• Equilibrium Phases: I-isotropic, N+I –nematic-isotropic coexistence, N*-chiral-nematic, and chiral-hierarchical mesophases: X-pattern, helical domains, and planar- nematic and homeotopic-nematic, and structural glass.

• Non-equilibrium: Shear-induced deformations of the orientation textures (in flow-vorticity plane)

• Soft-mode of charged chiral fibrous viruses (fd)

• Synchronized oscillations of dimers in biphasic phase of charged fibrous virus (fd) suspensions

• Flow-driven Mass Transports
  – Flow instability due to coupling of shear-gradients with concentration
  – Local interfacial migration of small particles in big droplets

• Protein Misfolding and Aggregations in the Low-frequency Electric-fields
  ALS-targeted protein-protein aggregation, ion-channel receptors, and the misfolding states of protein-receptor interactions are classified in terms of the conformational changes of polypeptides, and can be explored by means of image-time correlation and the relaxation times in the electro-optic modulation light scattering (EOM-LS).
  Statistical modeling of diffusion processes far out of equilibrium in crowded networks of cellular fibers and neuronal signaling as an active process.

Various phases and dynamical states are observed in suspensions of long and thin colloidal rods (fd‐virus particles) as the result of interactions between the charged rods through the polarization of electric double‐layers and the layer of condensed ions, electro‐ osmotic flow, as well as the association/dissociation of condensed ions [1].

More:

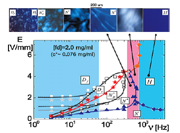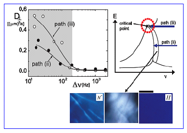
(Left) The phase/state diagram in the electric‐field amplitude‐versus‐frequency plane with depolarized images of phases/ states. (Right) Perpendicular diffusion constant for different pathways on approaching the critical frequency in the phase/state diagram.

The field-induced criticality is determined by measuring the time and domains as a function of frequency and amplitude. The critical exponent of field-induced criticality is found as a function of exponential power and logarithmic, depending on the pathways [2].

More:

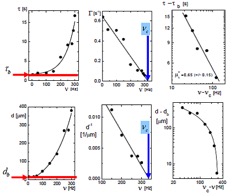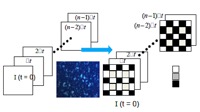
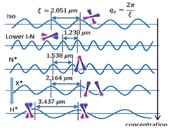
Image-time correlation spectroscopy and mesoscopic dynamics: A time series of depolarized CCD images is recorded, from which a time‐image intensity correlation function is constructed by averaging over all CCD‐pixels. The decay rate of the morphological changes is then quantified in the image-time correlations. [Refs: Kang and J.K.G. Dhont, EPJE 30, 333‐340 (2009), Journal of Biomedical Science and Engineering, 3, 625 – 632 (2010), and Kang, RSI 82, 053903 (2011)]. The characteristic time and domain size of small nematic domains in the electric field induced dynamical states.

Structural arrest as a result of particle-caging due to strong overlap of these extended double layers is observed by means of dynamic light scattering. The morphology of the system therefore consists of chiral-nematic domains with different orientations. Below the glass-transition concentration the initial morphology with large shear-aligned domains breaks up into smaller domains (in upper images), however, there is an initial caging in the glass concentration. [3, 4].

More:

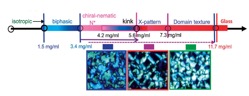
Decay rates of image-time correlations for far below the glass transition and the glass concentration, observed in dispersions of long and highly charged rod-like colloids (fd-virus particles). Equilibrium phase of charged fibrous virus (fd) suspensions: I-isotropic, N+I –nematic-isotropic coexistence, N*-chiral-nematic, and chiral-hierarchical mesophases: X-pattern, helical domains, and planar- nematic and homeotropic-nematic, and structural glass.

The electric-field induced dynamical states are shown with the oscillations of small-nematic domins (of 30 micron size), where the orientational order parameter is varied for various field conditions: amplitudes at a fixed frequency of 200 Hz and a fd-concentration of 2.0 mg/ml. [5, 6, 7, 8].

(Left) Real-image and (Right) animated intensity oscillations of the small-nematic domains in an electric field induced dynamical state.

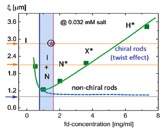
Anisotropic particles can exhibit either a continuous phase transition or the “freezing” of order parameter fluctuation. The collective soft-mode is observed with a finite cutoff dispersion where the relaxation time diverges in the microscopic dynamics of charged chiral fd-viruses, with a rotation restoring “twist“. [9].

(Left) Correlation length versus fd-rod concentration for various equilibrium phases, and (Right) the characteristic feature of correlation length in various equilibrium phases. the critical frequency in the phase/state diagram.

The glass transition (red-line) of long-ranged repulsive rods is characterized by the unique kinetic arrest of both the dynamics of domains that constitute the chiral-nematic orientational texture, as well as individual rods inside the domains. [10].

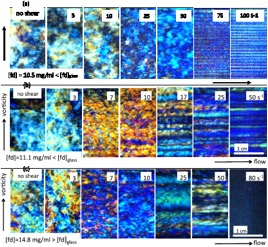
(Left) Shear-induced deformations of the orientation textures (in flow-vorticity plane) for various shear-rates and concentrations.(Right) Velocity profiles in the gradient of different fd-virus concentrations.

Micron-sized colloidal spheres are dispersed in an isotropic-nematic bi-phasic host suspension of charged rods (fd-virus particles), shown to spontaneously form dimers, which exhibit a synchronized oscillatory motion. [11].

Few snap shots of synchronized dimer oscillations in real space (Left) and Fourier K-space.

The interfacial migration due to Marangoni forces of clay particles within an oil droplet that is immersed in water, which is relevant for the formation kinetics of Pickering emulsions, compared with hydrophilic (MMT) and hydrophobic (OMT) clays. Here image-time correlations re employed to analyze the local migration for different types of clays inside the oil droplet [12].

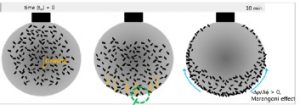
The simple cartoon of the interfacial migration due to Marangoni forces of clay particles within an oil droplet that is immersed in water, which is relevant for the formation kinetics of Pickering emulsions, and (right) the data movies of oil droplet in water interfaces, compared with hydrophilic (MMT) and hydrophobic (OMT) clays.